Deret Pangkat 2
selesaikan persamaan dibawa ini dengan metode deret pangkat.
penyelesainnya mirip dengan yang sebelumnnya, yakni kita misalkan.
a_nx^{n-2} "y'=\sum_{n=2}^{\infty}n(n-1)a_nx^{n-2}")
a_nx^{n-2} "\sum_{n=2}^{\infty}n(n-1)a_nx^{n-2}")
x^{n-2}+2\sum_{n=0}^{\infty}a_nx^{n+1}=0 "\sum_{n=2}^{\infty}n(n-1)x^{n-2}+2\sum_{n=0}^{\infty}a_nx^{n+1}=0")
kita misalkan
dan
(k+1)a_{k+2}&space;x^k+2\sum_{k=1}^{\infty}a_{k-1}x^k=0 "\sum_{k=0}^{\infty}(k+2)(k+1)a_{k+2} x^k+2\sum_{k=1}^{\infty}a_{k-1}x^k=0")
jika
(1)a_2&space;x^0=2a_2 "k=0\rightarrow (2)(1)a_2 x^0=2a_2")
(k+1)a_{k+2}x^k+2\sum_{k=1}^{\infty}a_{k-1}x^k=0 "2a_2+\sum_{k=1}^{\infty}(k+2)(k+1)a_{k+2}x^k+2\sum_{k=1}^{\infty}a_{k-1}x^k=0")
(k+1)a_{k+2}x^k+2a_{k-1}]x^k=0 "2a_2+\sum_{k=1}^{\infty}[(k+2)(k+1)a_{k+2}x^k+2a_{k-1}]x^k=0")
jelas bahwa
juga komponen yang harus nol adalah
(k+1)a_{k+2}+2a_{k-1}=0 "(k+2)(k+1)a_{k+2}+2a_{k-1}=0")
(k+1} "a_{k+2}=-\frac{2a_{k-1}}{(k+2)(k+1}")
sekarang kita subtitusi nilai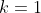
sampai 
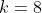maka di peroleh
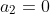
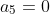
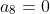
dengan demikian diperoleh 2 solusi yaitu
1.
2.
untuk kasus 1
=1-\frac{1}{3}x^3+\frac{1}{6}x^6-\frac{1}{1620}x^9+.......... "y_1(x)=1-\frac{1}{3}x^3+\frac{1}{6}x^6-\frac{1}{1620}x^9+..........")
untuk kasus 2
=x-\frac{1}{6}x^4+\frac{1}{126}x^7+.......... "y_2(x)=x-\frac{1}{6}x^4+\frac{1}{126}x^7+..........")
dengan demikian dapat ditulis secara lengkap
=a_0[1-\frac{1}{3}x^3+\frac{1}{6}x^6-\frac{1}{1620}x^9..........] "y_1(x)=a_0[1-\frac{1}{3}x^3+\frac{1}{6}x^6-\frac{1}{1620}x^9..........]")
=a_1[x-\frac{1}{6}x^4+\frac{1}{126}x^7+..........] "y_2(x)=a_1[x-\frac{1}{6}x^4+\frac{1}{126}x^7+..........]")
saya kira ini mudaji...
dan kalau ada pertanyaan, silahkan coment, pertannyaannya tentang tugas kulia juga boleh.
hehehehe nanti kita kerjakan sama-sama.
penyelesainnya mirip dengan yang sebelumnnya, yakni kita misalkan.
kita misalkan
jika
jelas bahwa
juga komponen yang harus nol adalah
sekarang kita subtitusi nilai
dengan demikian diperoleh 2 solusi yaitu
1.
2.
untuk kasus 1
untuk kasus 2
dengan demikian dapat ditulis secara lengkap
saya kira ini mudaji...
dan kalau ada pertanyaan, silahkan coment, pertannyaannya tentang tugas kulia juga boleh.
hehehehe nanti kita kerjakan sama-sama.
Komentar
Posting Komentar